Also available in: English

Johdanto Webmercatoriin

Johdanto

Mercator-projektio on ollut olemassa lähes 500 vuotta. Historiansa aikana sillä on ollut monia rooleja. Se alkoi vastauksena merenkulun tarpeisiin, jatkui de facto -projektiona atlaksissa, ja nyt mercator-projektio on kokenut uuden aamunkoiton webmercatorin muodossa, ollen kiistatta yhtä ajankohtainen kuin koskaan. Karttaprojektiot voivat olla hankala aihe. Olen kirjoittanut tämän artikkelin toivoen saavani itselleni selkeyttä aiheeseen. Tässä artikkelissa käyn läpi, miten mercator- ja erityisesti web mercator -kartta muodostuu ja mikä erottaa web mercator -kartan tavallisesta mercator-kartasta. Perusymmärrys trigonometriasta ja kalkyylista on suositeltavaa.

Projisointi pallolta 2D-pinnalle on kartografian perusongelma. Sitä ei ole mahdollista tehdä isometrisesti (ilman vääristymiä), joten kartta on aina kompromissi, joka yleensä keskittyy yhteen avainmittariin, jonka se näyttää totuudenmukaisesti. Yleisiä mittareita, joista kartografit ovat kiinnostuneita, ovat etäisyys, pinta-ala, muoto ja suunta. Mercator-projektio luokitellaan konformiseksi projektioksi, mikä tarkoittaa, että se säilyttää suunnan mutta ei etäisyyttä tai muotoa. Tämä aiheuttaa sen, että suora viiva Mercator-kartalla olisi loksodroma (kutsutaan myös rumbillinjaksi) pallolla.

Loksodroma, joka kulkee navalta navalle:

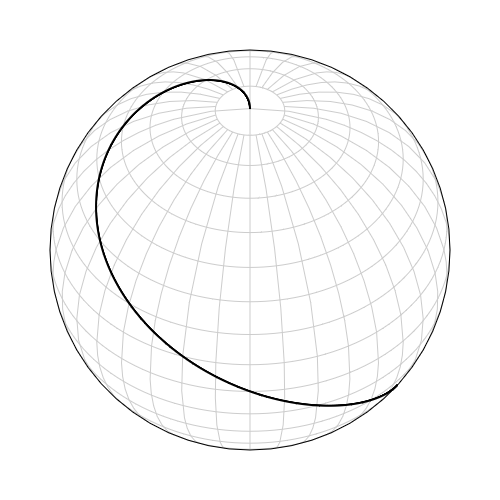
Tämä on optimaalista merenkulussa, koska voit helposti nähdä minne päädyt, kun pidät tietyn suuntiman. Haittapuolena se ei näytä pinta-aloja tasaisesti; alueet suurenevat mitä lähempänä napoja ollaan. Tämä on aiheuttanut kritiikkiä Mercator-projektiota kohtaan, koska se näyttää erityisesti Euroopan suurempana kuin se on suhteessa esimerkiksi Afrikkaan. Väittäisin, että ainakin 1500-luvulla mercator-projektio luotiin ratkaisuksi ajankohtaiseen merenkulun ongelmaan eikä nationalistisena propagandana.

Toinen kätevä ominaisuus, joka tulee konformisuuden mukana, on se, että koska Mercator säilyttää suunnan, se tarkoittaa, että pohjoinen on aina ylhäällä kartalla. Tämä saattaa kuulostaa hassulta, koska olemme nykyään niin tottuneita konformisiin projektioihin. Lisäksi kaikki leveyspiirit ja pituuspiirit ovat suoria viivoja.

Mittakaavakerroin

Konformisuuden säilyttämiseksi haluamme, että kaikissa kartan kohdissa yhden pituusasteasteen pituus on yhtä suuri kuin yhden leveysasteasteen pituus. Yhden leveysasteen etäisyys on vakio missä tahansa oletkin, koska kaikki vakiopituusviivat (meridiaanit) ovat isoympyröitä, joiden pituus on 2πR. Vakioleveyden viivat (leveyspiirit) eivät ole isoympyröitä, paitsi päiväntasaaja. Leveyspiirin pituus on yhtä suuri kuin päiväntasaajan pituus kerrottuna leveysasteen kosinilla (2πRcos).

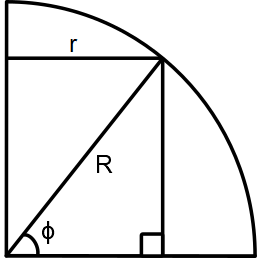
Nyt tiedämme, mikä on leveyspiirin pituus tietyssä pisteessä, ja nyt haluamme määrittää, miten lat/lon-arvot kartoitetaan x- ja y-koordinaatteihin kartalla. Mercator-kartassa kartan origo (piste 0,0) sijaitsee kartan keskellä, antaen meille potentiaalisen koordinaattialueen ([-90,90],[-180,180]). X-akseli on päiväntasaaja ja y-akseli on nollameridiaani. X-akselin pituus on 2πR ja meidän täytyy määrittää y-akselin pituus. Tämän määrittämiseksi meidän täytyy laskea niin sanottu mittakaavakerroin tietylle leveyspiirille. Kuten aiemmin määriteltiin, tietyllä leveysasteella on pituus 2πRcos. Siksi saadaksemme kunkin leveyspiirin pituudeksi 2πR, meidän täytyy kertoa leveyspiirin pituus 2πR/2πR cos(x) = 1/cos(x). Kosinin käänteislukua kutsutaan myös sekantiksi (sec(x)=1/cos(x)). Nyt pääsemme mercator-projektion matemaattiseen ytimeen. Saadaksemme leveyspiirin mittakaavakertoimen leveysasteella x, meidän täytyy summata kaikki 1/cos(x):t matkan varrelta. Jos on opiskellut kalkyylisä, on nyt selvää, että tämä voidaan saavuttaa integraalilla: ∫sec(x).

Sekantin integraali

Mittakaavakertoimen ja siten sekantin integraalin laskeminen on historiallisesti ollut pääongelma mercator-projektion kanssa, ja sen löytäminen on melko mielenkiintoinen tarina. Aion kirjoittaa siitä oman blogikirjoituksen, mutta sillä välin voit tutustua tähän erinomaiseen Lior Sinain blogikirjoitukseen aiheesta.

Johdetaan kaava sekantin integraalille, koska ainakin minulle se ei ole kovin intuitiivinen. On useita tapoja johtaa kaava (merkittävimmin substituutio, osittaismurtoluvut, trigonometriset kaavat, hyperboliset funktiot). Minulle substituutiomenetelmä on aina ollut helpoin ymmärtää:

Käytämme substituutiota u = sec x + tan x.
Koska sec x:n (sec x tan x) ja tan x:n (sec^2x) derivaatoilla on sec x yhteisenä tekijänä, saamme
du = sec x tan x + sec^2x.

Nyt:
∫ sec x dx
= ∫ sec x (sec x + tan x) / (sec x + tan x) dx
= ∫ (sec^2x + sec x tan x) / (sec x + tan x) dx
Sijoittamalla u yllä olevaan integraaliin saamme
∫ du / u = ln |u| + C
Ja nyt sijoittamalla u = sec x + tan x takaisin saamme
ln |sec x + tan x| + C

Ln | sec x + tan x | C:n lisäksi sekantin integraalilla on kaksi muuta ekvivalenttia trigonometrista identiteettiä: ½ ln((1+sin x)/(1-sin x))+C ja ln | tan (x/2 + π/4) |. Yleensä käytetään sitä identiteettiä, joka on kätevin (kuten alla olevassa esimerkissä on esitetty)

Erot mercatorin ja webMercatorin välillä

Jos olet seurannut tarkkaavaisesti, saatat nyt mainita, että kyllä tämä toimii täysin pyöreällä pallolla, mutta Maa ei ole täydellinen pallo, vaan ellipsoidi, joka on hieman litistynyt navoilta ja pullistunut päiväntasaajalta. Mercator-projektio ottaa tämän huomioon, mutta webMercator ei. Tällä ei olisi muuten väliä, mutta webMercator vaatii koordinaattiensa olevan WGS84:ssä, joka olettaa ellipsoidimaapallon. Tämä aiheuttaa webMercatorin olevan hieman epäkonforminen. Vääristymä on suurempi mitä lähempänä napoja ollaan. Tästä syystä esimerkiksi Yhdysvaltain puolustusministeriö ei hyväksy webMercatoria käytettäväksi missään virallisessa käytössä.

Mainitsin aiemmin, että asettamalla kartan origon kohtaan (0,0), meillä on potentiaalinen koordinaattialue ([-90,90],[-180,180]). Kuitenkin koska mittakaavakerroin lähestyy ääretöntä, kun leveysasteen itseisarvo lähestyy 90:tä, meidän täytyy rajata y-akselin alue tiettyyn arvoon. Internet-karttasovellukset näyttävät yleensä karttansa neliömäisinä laattoina. Laatta zoomitasolla 0 kattaa koko maailman. Siksi webMercatorissa valitaan sellaiset koordinaatit, että tuloksena oleva kartta on neliö. Tämä voidaan laskea ratkaisemalla x yhtälöstä 2πR = 2Rln|tan(π/4 + x/2)|:

2πR = 2Rln[tan(π/4 + x/2)]
π = ln[tan(π/4 + x/2)]
e^π = tan(π/4 + x/2)
arctan(e^π) = π/4 + x/2
x = 2arctan(e^π) - π/2 ≈ 85.05112878°

Joten jos haluamme näyttää maapallon neliönä pallopintaisessa mercator-projektiossa, meidän täytyy rajata y-akseli arvoon ±85.05112878°.

Toinen huomioitava asia webMercatorissa on, että sen origo ei ole kartan keskellä, vaan vasemmassa yläkulmassa. Tämä johtuu siitä, että monissa web-kehityksen tapauksissa elementtien origo on vasemmassa yläkulmassa.

Kuten mainittu, mercator ja webmercator eivät ole täydellisiä, mutta niitä käytetään silti useimmissa suosituissa web-karttasovelluksissa. Jos olet lukenut loppuun asti, kiitos lukemisesta, kaikki kommentit ovat aina tervetulleita.